尾递归优化
一个简单的递归函数:
def fibonacci(n): if n <= 1: return 1 return fibonacci(n-1) + fibonacci(n-2)
这个函数实现了一个裴波那契数列.非常简单,代码只有 3 行,但如果跟着函数运行的轨迹走.会发现这个函数背后的调用过程非常的复杂.每次递归都会依赖前面两次计算的结果.随着递归的层级上升,每次都会重新去调用前两次计算产生的结果.为了简化描述,下面是以 fibonacci(5) 模拟递归调用过程.
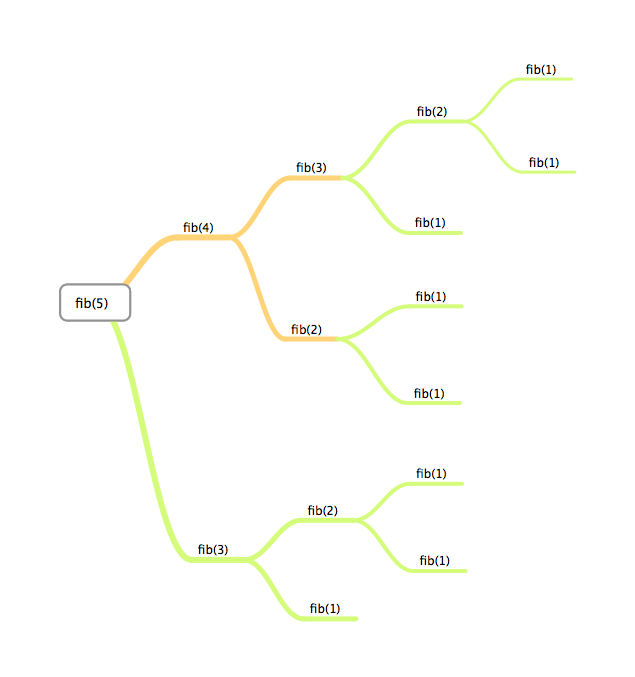
可以看到,每次递归都会重复前两次的调用过程.实际上这个递归数列并不需要每次都重复去求前两次的结果.如果用压栈的方法,一遍递归就可以搞定了.
def fibonacci(n): L = fibonacci.L if n <= 2: return L[-1] #get top else: n2 = L.pop() n1 = L.pop() L.append(n2) #'append' is stack's push L.append(n1+n2) return fibonacci(n-1) fibonacci.L = [1,1]
上面的代码耍了一个小花招.首先先设定好两个初始的计算结果,然后开始递归迭代.与前一版本递归不同的是,前一个递归需要在进入到递归底部后,才开始跳出来计算每一步递归后的结果,直到返回.而后一个递归会在最开始递归进入时就开始计算,进入到递归底部后(也就是 n <= 2)最终的结果就已经计算出来了,直接一层一层返回这个结果就可以了. 为了便于说明下面代码是利用两个变量做中间结果的版本:
def fib(n, n1=1, n2=1): if n < 2: return n1 return fib(n-1, n2, n1+n2)
跟上面那个压栈的方式一样.先设定好两个默认的结果,在递归进入时直接将结果计算出来并保存好. 下面是这个函数的调用过程:
fib(n = 10, n1 = 1, n2 = 1) fib(n = 9, n1 = 1, n2 = 2) fib(n = 8, n1 = 2, n2 = 3) fib(n = 7, n1 = 3, n2 = 5) fib(n = 6, n1 = 5, n2 = 8) fib(n = 5, n1 = 8, n2 = 13) fib(n = 4, n1 = 13, n2 = 21) fib(n = 3, n1 = 21, n2 = 34) fib(n = 2, n1 = 34, n2 = 55) fib(n = 1, n1 = 55, n2 = 89)